理解向量
向量具有維度和方向。例如，下圖描繪了一個二維向量 ，在笛卡爾座標系統中以箭頭表示。
向量 的頭部位於點 。(x 座標值為 ，y 座標值為 )。座標也稱為向量的分量。
相似度
可以使用幾個數學公式來確定兩個向量是否相似。其中最直觀且易於理解的是餘弦相似度。請考慮以下顯示三組圖表的圖像
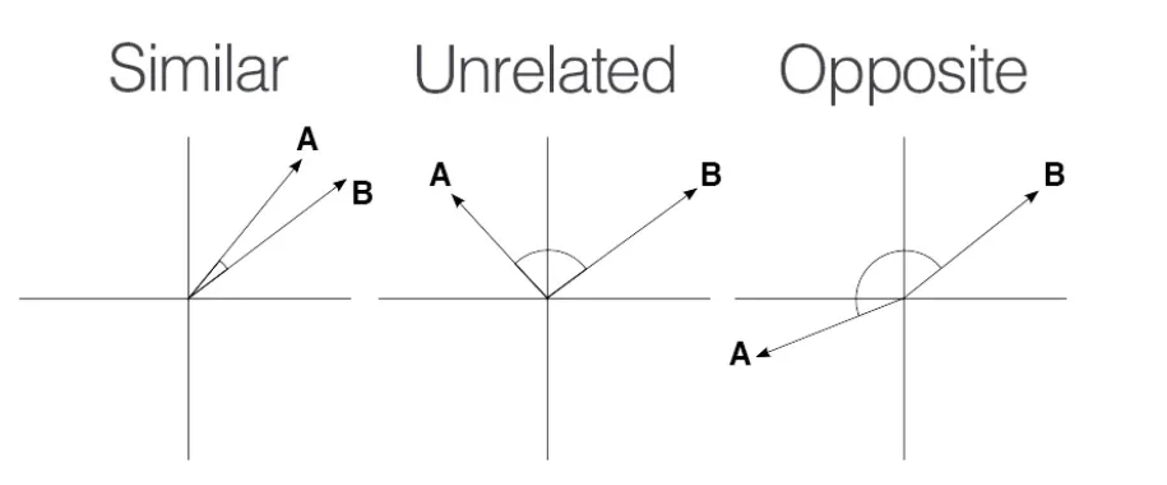
向量 和 在指向彼此靠近時，例如在第一張圖中，被認為是相似的。當向量彼此垂直指向時，被認為是不相關的，而當它們彼此遠離指向時，則被認為是相反的。
它們之間的角度 是衡量它們相似性的良好指標。角度 應如何計算？
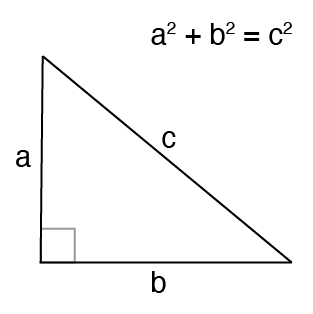
我們都熟悉畢氏定理。
當 a 和 b 之間的角度不是 90 度時呢？
請看餘弦定理。
下圖以向量圖形式顯示了這種方法：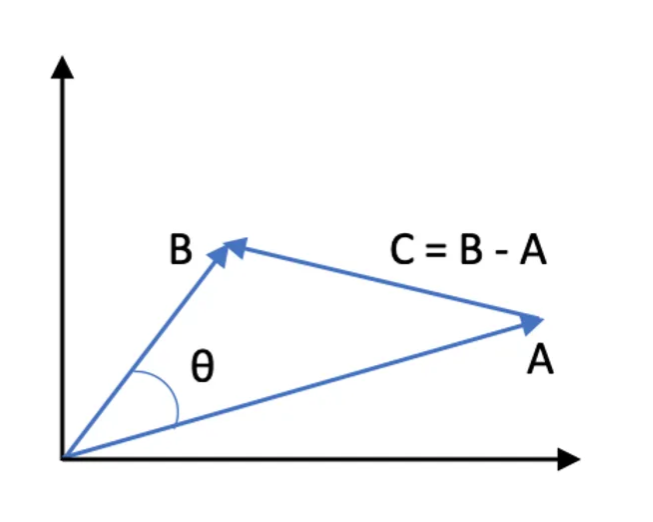 
此向量的大小根據其分量定義為
兩個向量 和 的點積根據其分量定義為
使用向量大小和點積重新寫出餘弦定理，得到以下結果
用 為 ，得到以下結果
此公式適用於高於 2 或 3 的維度，儘管很難視覺化。然而，可以在一定程度上視覺化。在 AI/ML 應用中，向量通常具有數百甚至數千個維度。
以下顯示使用向量分量在更高維度中的相似度函數。它透過使用加總數學語法，將先前給定的二維大小和點積定義擴展到 N 維。
這是向量儲存簡單實作中使用的關鍵公式，可以在 SimpleVectorStore 實作中找到。
